GPTQ：从量化谈起

模型量化是一种压缩网络参数的方式，它将神经网络的参数（weight）、特征图（activation）等原本用浮点表示的量值换用定点（整型）表示，在计算过程中，再将定点数据反量化回浮点数据，得到结果。模型量化实现建立在深度网络对噪声具有一定的容忍性上，模型量化相当于对深度网络增加了一定的噪声（量化误差），如果量化位数合适，模型量化基本不会造成较大的精度损失。
量化模型实现加速，不仅仅由于整形运算比浮点运算更快，我更倾向于加速了对权重的读取（访存加速），尤其是以大模型LLM的部署为例，Self-Decoder 阶段就是典型的 Memory-Bound 的操作。其余的加速方式，要依赖于量化算子优化、量化图优化等方面。

量化

量化对象

可以对模型参数（weight）、激活值（activation）或者梯度（gradient）做量化。
通常而言，模型的参数分布较为稳定，因此对参数 weight 做量化较为容易。
然而，模型的激活值往往存在异常值，直接对其做量化，会降低有效的量化格点数，导致精度损失严重，因此，激活值的量化需要更复杂的处理方法（如 SmoothQuant）。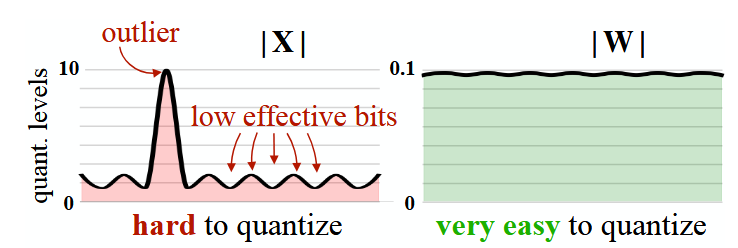
quan_weight.png

线性量化下，浮点数与定点数之间的转换公式

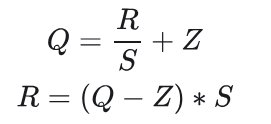
quan_cal.png

  • R 表示量化前的浮点数
  • Q 表示量化后的定点数
  • S（Scale）表示缩放因子的数值
  • Z（Zero）表示零点的数值
    v2-1ce8aece0beba9dae4e7aaf6a64d4f6d_1440w.png
    图中展示的是量化到 int8，因此 Round to Grid 实际上是先乘以 127(=2**(8-1)-1)，然后 round 到最近的整数。

对称量化、不对称量化

对称量化（如左图所示）中，量化前后的 0 点是对齐的，因此不需要记录零点。它适合对分布良好且均值为 0 的参数进行量化。因此对称量化常用于对 weight 量化。
非对称量化（如右图所示）中，量化前后 0 点不对齐，需要额外记录一个 offset，也就是零点。非对称量化常用于对 activation 做量化。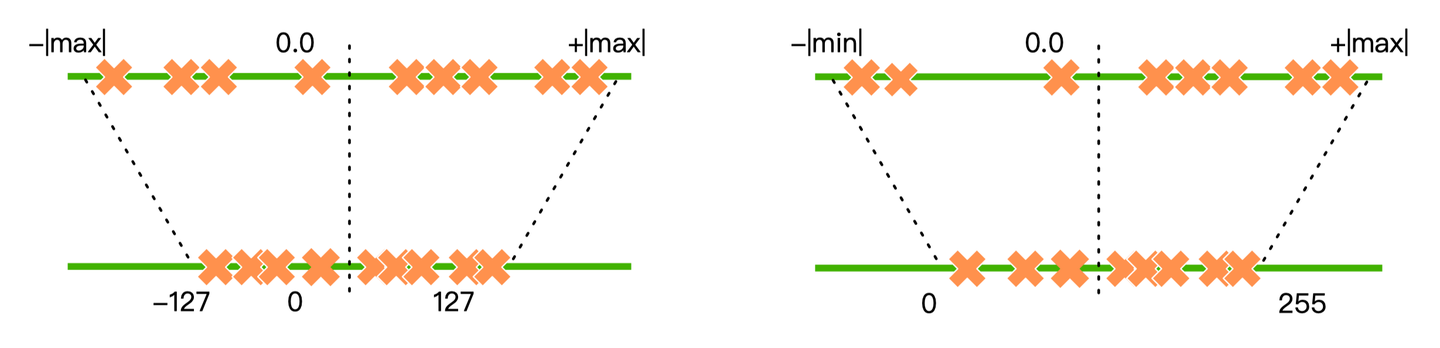
v2-6f905bb60c96753b5dd82820db5a65d7_1440w.png

PTQ and QAT

  • QAT（Quant-Aware Training） 也可以称为在线量化（On Quantization）。它需要利用额外的训练数据，在量化的同时结合反向传播对模型权重进行调整，意在确保量化模型的精度不掉点。
  • PTQ （Post Training Quantization）也可以称为离线量化（Off Quantization）。它是在已训练的模型上，使用少量或不使用额外数据，对模型量化过程进行校准，可能伴有模型权重的缩放。其中：
  • 训练后动态量化（Post Dynamic Quantization）不使用校准数据集，直接对每一层 layer 通过量化公式进行转换。QLoRA 就是采用这种方法。
  • 训练后校正量化（Post Calibration Quantization）需要输入有代表性的数据集，根据模型每一层 layer 的输入输出调整量化权重。GPTQ 就是采用这种方法。本质上 PTQ 就是在校准过程中，研究不同的metric来更好地选择截断上下界。例如常见的 MinMax，Histogram，Entropy等，也有一些基于 search 的方法来遍历探索。不同场景不同网络适合的metrci 各不相同，校准集的选择也会对结果有所影响，需要在实际应用中尝试不同的组合来获得最好的效果。
    在实际应用中，更为常用的是PTQ的方法，大部分芯片厂商自己的编译器，已经集成了基础的PTQ方法，并与算子融合图优化等组合使用，对绝大部分模型能获得精度与速度都令人满意的结果。只有少部分特殊的模型结构场景，或更低bit量化的量化需求情况下才会考虑QAT的方法。

GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers

GPTQ 对某个 block 内的所有参数逐个量化，每个参数量化后，需要适当调整这个 block 内其他未量化的参数，以弥补量化造成的精度损失。GPTQ 量化需要准备校准数据集。
GPTQ 的思想最初来源于 Yann LeCun 在 1990 年提出的OBD算法，随后OBS、OBC（OBQ） 等方法不断进行改进，而 GPTQ 是 OBQ 方法的加速版。GPTQ 的量化有严谨的数学理论推导，所有的算法步骤都有理论支撑。为了理解 GPTQ 的思想，我们需要先介绍 OBD -> OBS -> OBQ 的演进过程。

OBD：Optimal Brain Damage

关于神经网络剪枝算法的论文，主要利用二阶导数信息度量模型参数的显著性，也就是度量模型删除参数对模型结果的影响，剪掉影响小的参数降低模型复杂度提高泛化能力。
具体算法流程为

  1. 搭建神经网络
  2. 训练神经网络至损失函数收敛
  3. 计算神经网络每个参数的二阶导数
  4. 计算神经网络每个参数的显著性
  5. 按照显著性对参数进行排序，并删除一些低显著性的参数。可认为删除参数是将其设置为0并训练时冻结。
  6. 从步骤2 开始重复
    该算法需要重复训练、剪枝操作，这同我们理解的训练后大语言模型量化似乎差的很远。但带来了通过神经网络参数二阶导数来评估参数对模型结果影响核心想法。

构建神经网络目标函数在局部点(参数)上扰动的二阶近似函数。
首先在指定参数位置对损失函数做泰勒二阶展开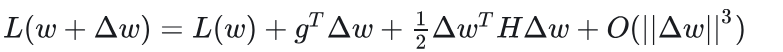
image.png
参数w变化带来的损失函数扰动表示为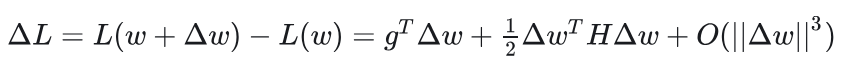
image.png
在OBD论文中这部分公式写成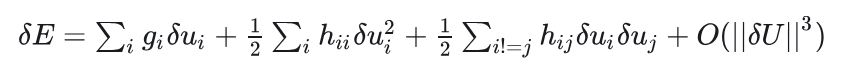
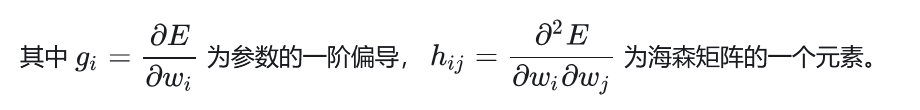
image.png
image.png
image.png
于是，上式可以简化成：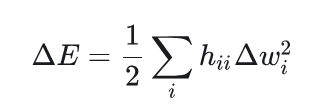
image.png
由此可以得到删除一个参数，对目标函数的影响。所以只需要计算海森矩阵，就可以知道每个参数对目标的影响。然后就可以按照影响从小到大给参数排个序，这样就确定了参数剪枝的次序。

OBS：Optimal Brain Surgeon

OBS 认为，参数之间的独立性不成立，我们还是要考虑交叉项，因此上式变成了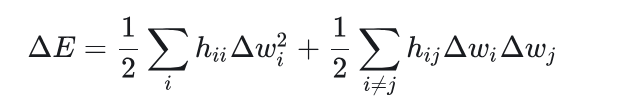
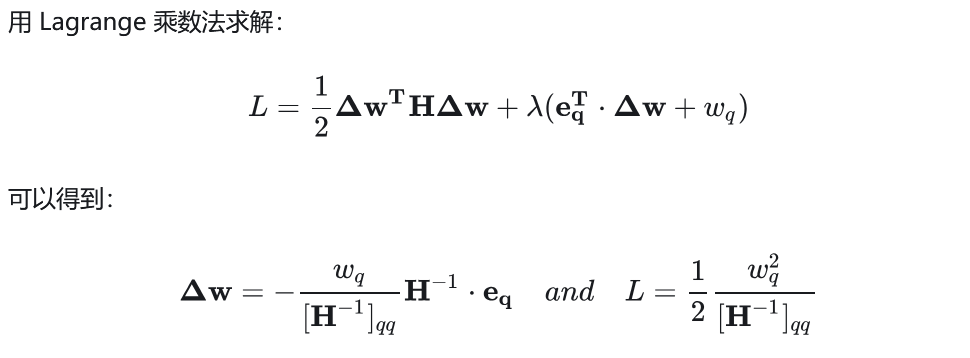
image.png
image.png
image.png
于是，也只需要求解海森矩阵的逆，就可以计算每个参数对目标的影响 ，然后就可以按照影响从小到大给参数排个序，这样就确定了参数剪枝的次序。同时，每次剪枝一个参数，其他的参数也按照δw更新一次。
这里的思想一直沿用到了 GPTQ 算法：也就是对某个 block 内的所有参数逐个量化，每个参数量化后，需要适当调整这个 block 内其他未量化的参数，以弥补量化造成的精度损失。

OBC

OBD 和 OBS 都存在一个缺点，就是剪枝需要计算全参数的海森矩阵（或者它的逆矩阵）。但在动辄上亿参数的神经网络下求解海森矩阵显然不可能。于是，我们可以假设参数矩阵的同一行参数互相之间是相关的，而不同行之间的参数互不相关，这样，海森矩阵就只需要在每一行内单独计算。
image.png
v2-d178e091e2068ba9256589f41acfc0d8_1440w.png
从 for 循环开始逐行分析：

  • Line 1：找到对目标函数影响最小的参数 p
  • Line 2：对参数 p 剪枝，并更新其他参数
  • Line 3：删除海森矩阵的 p 行 p 列，再求逆（这里用了数学的等价表达，降低了计算复杂度）

OBQ

OBQ （和OBC是同一篇文章）指出，剪枝是一种特殊的量化（即剪枝的参数等价于量化到 0 点），我们只需要修改一下 OBC 的约束条件即可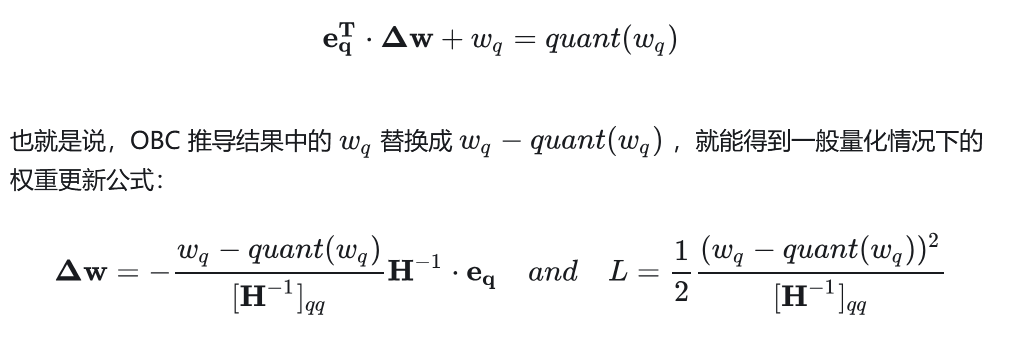
image.png
v2-76796d5d98dc3cc27254d33199ea1ddc_1440w.png

GPTQ

GPTQ 的创新点有：

  • OBS 采用贪心策略，先量化对目标影响最小的参数；但 GPTQ 发现直接按顺序做参数量化，对精度影响也不大。
  • 这项改进使得数矩阵每一行的量化可以做并行的矩阵计算，在大模型环境下，这项改进使得量化速度快了一个数量级；
  • Lazy Batch-Updates，延迟一部分参数的更新，它能够缓解 bandwidth 的压力；
  • Cholesky Reformulation，用 Cholesky 分解求海森矩阵的逆，在增强数值稳定性的同时，不再需要对海森矩阵做更新计算，进一步减少了计算量。
    关注第二个创新点，也就是 Lazy Batch-Updates 是如何缓解 bandwidth 的压力的。
    问题：虽然 GPTQ 降低了时间复杂度，但这个算法的计算/通信比太低，通信带宽成为了瓶颈。
    例如在量化某个参数矩阵的情况下，每次量化一个参数，其他所有未量化的参数都要按公式全都要更新一遍：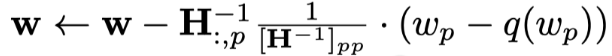
    v2-8cb25fd928d330bdaeef34af63b1da4f_1440w.png
    如果每行的量化并行计算，那么每次更新过程就需要 read + write 一次参数矩阵。如果参数矩阵的维度为k \times k，那么量化这个参数矩阵就需要读写 k 次参数，总共的 IO 量为k^3个元素。当 k 比较大时（>= 4096），需要读写的元素就非常多了，运行时间大都被 IO 占据。
    思路：由于参数量化是一列一列按次序进行的，第 i 列的参数的量化结果受到前 i-1 列量化的影响，但第 i 列的量化结果不影响前面列的量化。因此我们不需要每次量化前面的列，就更新一遍第 i 列的参数，而是可以先记录第 i 列的更新量，在量化到第 i 列时，再一次性更新参数，这样就可以减少 IO 的次数。

具体实现：将参数矩阵按每 128 列划分为一个个 group，量化某一列时，group 内的参数立即更新，而 group 后面的列只记录更新量，延迟更新。当一个 group 的参数全部量化完成，再统一对后面的所有参数做一次更新。这就是 Lazy Batch-Updates。
Lazy Batch-Updates 不减少实际的计算量，但它能有效解决吞吐的瓶颈问题。

代码

GPTQ_MODEL实现方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
@torch.inference_mode()
    def quantize(
        self,
        blocksize=128,
    ):
        # self.H = self.H.to(device=CUDA_0)
        # log.info(f"Quantization `{self.name}` using samples: `{self.nsamples}`")
        start = time.time()

        self.hessian_inverse = torch_compile(self.hessian_inverse)

        # process buffered inputs
        if len(self.fwd_inputs_buffered_data) > 0:
            torch_sync(device=self.module.target_device)

            for inp in self.fwd_inputs_buffered_data:
                self.process_batch(inp)

            # release buffer
            del self.fwd_inputs_buffered_data

        # if self.device.type not in ["mps", "cpu"]:
        #     self.module.weight.data = self.module.weight.data.cpu()

        # TODO: waiting for pytorch implementation of ops for MPS
        if sys.platform == "darwin" and os.getenv("PYTORCH_ENABLE_MPS_FALLBACK") != "1":
            raise RuntimeError("For MacOS you must set env `PYTORCH_ENABLE_MPS_FALLBACK=1` before running quantization.")

        if self.module_copy is None:
            # log.info("copy W to cuda_1")
            W = self._clone_module(device=self.module.target_device)
        else:
            W = self.module_copy.to(device=self.module.target_device)
            del self.module_copy

        self.quantizer.find_params(W, weight=True)

        H = self.H.to(device=self.module.target_device)
        del self.H

        dead = torch.diag(H) == 0
        H[dead, dead] = 1
        W[:, dead] = 0

        # g_idx = []
        scale = []
        zero = []
        now_idx = 1

        if self.qcfg.static_groups:
            import copy

            groups = []
            for i in range(0, self.columns, self.qcfg.group_size):
                quantizer = copy.deepcopy(self.quantizer)
                quantizer.find_params(W[:, i : (i + self.qcfg.group_size)], weight=True)

                scale.append(quantizer.scale)
                zero.append(quantizer.zero)
                groups.append(quantizer)

        if self.qcfg.desc_act:
            perm = torch.argsort(torch.diag(H), descending=True)
            W = W[:, perm]
            H = H[perm][:, perm]
            invperm = torch.argsort(perm)

        if hasattr(self.qcfg, "hyb_act") and self.qcfg.hyb_act and not self.qcfg.desc_act:
            from .gar import compute_local_perms, compute_global_perm, compose_final_perm
            local_perms = compute_local_perms(torch.diag(H), self.qcfg.group_size)
            global_perm = compute_global_perm(torch.diag(H), self.qcfg.group_size)
            final_perm = compose_final_perm(local_perms, global_perm, self.qcfg.group_size)
            W = W[:, final_perm]
            H = H[final_perm][:, final_perm]

        Losses = torch.zeros_like(W)
        Q = torch.zeros_like(W)

        Hinv, damp = self.hessian_inverse(H)

        for i1 in range(0, self.columns, blocksize):
            i2 = min(i1 + blocksize, self.columns)
            count = i2 - i1

            W1 = W[:, i1:i2].clone()
            Q1 = torch.zeros_like(W1)
            Err1 = torch.zeros_like(W1)
            Losses1 = torch.zeros_like(W1)

            if Hinv is not None:
                Hinv1 = Hinv[i1:i2, i1:i2]

            for i in range(count):
                w = W1[:, i]
                if Hinv is not None:
                    d = Hinv1[i, i]

                if self.qcfg.group_size != -1:
                    if not self.qcfg.static_groups:
                        if (i1 + i) % self.qcfg.group_size == 0:
                            self.quantizer.find_params(W[:, (i1 + i) : (i1 + i + self.qcfg.group_size)], weight=True)

                        if ((i1 + i) // self.qcfg.group_size) - now_idx == -1:
                            scale.append(self.quantizer.scale)
                            zero.append(self.quantizer.zero)
                            now_idx += 1
                    else:
                        idx = i1 + i
                        if self.qcfg.desc_act:
                            idx = perm[idx]

                        self.quantizer = groups[idx // self.qcfg.group_size]

                q = self.quantizer.quantize(w.unsqueeze(1)).flatten()
                Q1[:, i] = q
                if Hinv is not None:
                    Losses1[:, i] = (w - q) ** 2 / d**2
                    err1 = (w - q) / d
                    W1[:, i:] -= err1.unsqueeze(1).matmul(Hinv1[i, i:].unsqueeze(0))
                    Err1[:, i] = err1

            Q[:, i1:i2] = Q1
            if Hinv is not None:
                Losses[:, i1:i2] = Losses1 / 2
                W[:, i2:] -= Err1.matmul(Hinv[i1:i2, i2:])

        # TODO: why is there a torch_sync here? There are no streaming ops here?
        # torch_sync(device=self.module.target_device)

        if Hinv is not None:
            del Hinv
            if self.nsamples != 0:
                avg_loss = torch.sum(Losses).item() / self.nsamples

                if math.isnan(avg_loss):
                    print("Losses sum item:", torch.sum(Losses).item())
                    raise ValueError(f"Quantization: Failed due to `NaN` loss for `{self.name}`")
            else:
                log.warn(f"Quantization: `{self.name}` is not activated due to model inference logic (MoE)")
                avg_loss = 999999999
        else:
            avg_loss = 999999999

        del Losses

        group_size = self.qcfg.group_size if self.qcfg.group_size != -1 else self.columns

        if self.qcfg.static_groups and self.qcfg.desc_act:
            g_idx = [perm[i] // group_size for i in range(self.columns)]
        else:
            g_idx = [i // group_size for i in range(self.columns)]

        g_idx = torch.tensor(g_idx, dtype=torch.int32, device=Q.device)

        if self.qcfg.desc_act:
            Q = Q[:, invperm]
            g_idx = g_idx[invperm]

        if hasattr(self.qcfg, "hyb_act") and self.qcfg.hyb_act and not self.qcfg.desc_act:
            from .gar import invert_perm
            inv_final = invert_perm(final_perm)
            Q = Q[:, inv_final]
            inv_global_perm = invert_perm(global_perm)
            inv_global_perm_list = inv_global_perm.tolist()
            temp_scale = [ scale[i] for i in inv_global_perm_list ]
            scale = temp_scale
            temp_zero = [ zero[i] for i in inv_global_perm_list ]
            zero = temp_zero

        if isinstance(self.module, transformers.Conv1D):
            Q = Q.t()

        if Q.shape != self.module.weight.shape:
            Q = Q.reshape(self.module.weight.shape).type_as(self.module.weight.data)
        else:
            Q = Q.type_as(self.module.weight.data)

        #Q = Q.to(device=use_device)

        if scale == []:
            scale.append(self.quantizer.scale)
            zero.append(self.quantizer.zero)

        scale = torch.cat(scale, dim=1)
        zero = torch.cat(zero, dim=1)

        duration = time.time() - start

        return Q, scale, zero, g_idx, duration, avg_loss, damp, self.nsamples
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
+-----------------------------+
| 开始量化过程                |
+-----------------------------+
               |
               v
+-----------------------------+
| 初始化变量和参数            |
| - blocksize = 128           |
| - 记录开始时间              |
+-----------------------------+
               |
               v
+-----------------------------+
| 编译 Hessian 逆矩阵         |
| - self.hessian_inverse =    |
|   torch_compile(self.hessian_inverse)
+-----------------------------+
               |
               v
+-----------------------------+
| 处理缓冲输入数据            |
| - 如果有缓冲数据，逐个处理   |
| - 清空缓冲数据              |
+-----------------------------+
               |
               v
+-----------------------------+
| 检查平台和环境变量          |
| - 如果是 MacOS 平台且未设置 |
|   PYTORCH_ENABLE_MPS_FALLBACK |
|   抛出错误                  |
+-----------------------------+
               |
               v
+-----------------------------+
| 复制权重矩阵 W              |
| - 如果 module_copy 为 None，|
|   克隆模块到目标设备        |
| - 否则，使用 module_copy    |
+-----------------------------+
               |
               v
+-----------------------------+
| 初始化量化器参数            |
| - self.quantizer.find_params(W, weight=True)
+-----------------------------+
               |
               v
+-----------------------------+
| 处理 Hessian 矩阵           |
| - 将 Hessian 矩阵移动到目标设备 |
| - 删除原始 Hessian 矩阵      |
| - 处理 Hessian 矩阵的对角线 |
+-----------------------------+
               |
               v
+-----------------------------+
| 初始化变量                  |
| - scale, zero, now_idx      |
+-----------------------------+
               |
               v
+-----------------------------+
| 检查是否使用静态分组        |
| - 如果是，计算分组参数       |
+-----------------------------+
               |
               v
+-----------------------------+
| 检查是否使用描述性激活      |
| - 如果是，对权重矩阵和 Hessian 矩阵进行排序 |
+-----------------------------+
               |
               v
+-----------------------------+
| 检查是否使用混合激活        |
| - 如果是，计算局部和全局排列 |
+-----------------------------+
               |
               v
+-----------------------------+
| 初始化损失矩阵和量化矩阵    |
| - Losses 和 Q 初始化为零矩阵 |
+-----------------------------+
               |
               v
+-----------------------------+
| 计算 Hessian 逆矩阵         |
| - Hinv, damp = self.hessian_inverse(H)
+-----------------------------+
               |
               v
+-----------------------------+
| 按块处理权重矩阵            |
| - 遍历每一块，量化并更新权重 |
+-----------------------------+
               |
               v
+-----------------------------+
| 计算平均损失                |
| - 如果 Hinv 不为 None，计算平均损失 |
| - 否则，设置平均损失为极大值 |
+-----------------------------+
               |
               v
+-----------------------------+
| 清理资源                    |
| - 删除 Losses 矩阵           |
+-----------------------------+
               |
               v
+-----------------------------+
| 计算分组索引                |
| - 根据配置计算分组索引       |
+-----------------------------+
               |
               v
+-----------------------------+
| 处理权重矩阵的排列          |
| - 如果使用描述性激活或混合激活，反转排列 |
+-----------------------------+
               |
               v
+-----------------------------+
| 调整量化矩阵形状            |
| - 确保 Q 的形状与模块权重一致 |
+-----------------------------+
               |
               v
+-----------------------------+
| 返回量化结果                |
| - Q, scale, zero, g_idx, duration, avg_loss, damp, self.nsamples |
+-----------------------------+

参考链接：
https://zhuanlan.zhihu.com/p/646210009
https://zhuanlan.zhihu.com/p/680567656
https://zhuanlan.zhihu.com/p/629517722
https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=17c0a7de3c17d31f79589d245852b57d083d386e
https://readpaper.feishu.cn/docx/OPP2dTuXAoaO0oxWhQAcC05Wnpc
https://github.com/ModelCloud/GPTQModel/blob/main/gptqmodel/quantization/gptq.py